The correct answer is: a) Tyriq's only
Let's analyze both interpretations:
Tyriq's interpretation:
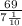 represents the length of the section if the roof is 7 1/10 m across.
represents the length of the section if the roof is 7 1/10 m across.
Corbin's interpretation:
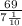 represents the number of solar panels that would fit if each panel was 7 1/10 m long.
represents the number of solar panels that would fit if each panel was 7 1/10 m long.
To check which interpretation makes sense, we need to look at the units.
The area of the roof is given in square meters (m²), and the length of the section is in meters (m). So, we are looking for a length value.
Let's perform the division:
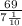 .
.
![\[ (69)/(7(1)/(10)) = (69)/((71)/(10)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8fq64bchltgwxw9wd2gxkw1ks4bq9vd2yg.png)
To divide by a fraction, multiply by its reciprocal:
![\[ (69)/((71)/(10)) \cdot (10)/(1) = (690)/(71) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/hno0yx6ham93qt656jmynpvq07g6qsgpeo.png)
This result represents the length of the section in meters. Therefore, Tyriq's interpretation makes sense in this context.