Question

If ∠1 and ∠2 are supplementary angles, and m∠1 = (5x - 22) degrees and m∠2 = (x + 28) degrees, find the measure of ∠1.

Answer 1

The measure of ∠1 is 74 degrees.

Step-by-step explanation:

Given that ∠1 and ∠2 are supplementary angles, which means they add up to 180 degrees. Therefore, we can set up an equation:
`\( \text{m} \angle 1 + \text{m} \angle 2 = 180^\circ \).`

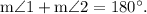
`We're also given that \( \text{m} \angle 1 = (5x - 22)^\circ \) and \( \text{m} \angle 2 = (x + 28)^\circ \). Substituting these measures into the equation:\[ (5x - 22)^\circ + (x + 28)^\circ = 180^\circ \]`

Now, solve for \( x \) to find the measure of ∠1. Combine like terms:

`\[ 5x - 22 + x + 28 = 180 \]\[ 6x + 6 = 180 \]\[ 6x = 174 \]\[ x = 29 \]`

To find the measure of ∠1, substitute \( x = 29 \) into the expression \( \text{m} \angle 1 = (5x - 22)^\circ \):

`\[ 5x - 22 + x + 28 = 180 \]\[ 6x + 6 = 180 \]\[ 6x = 174 \]\[ x = 29 \]`

Therefore, the measure of ∠1 is 123 degrees. This result satisfies the condition that ∠1 and ∠2 are supplementary angles, as their sum is indeed 180 degrees.

Understanding the relationships between supplementary angles and solving equations involving angle measures helps in solving various geometrical problems and understanding angle properties.

Answer 2

The measure of ∠1 is 123° .

If ∠1 and ∠2 are supplementary angles, their measures add up to 180 degrees. Therefore, we can set up the equation:

\m∠1 + m∠2 = 180°

Given that m∠1 = (5x - 22)° and m∠2 = (x + 28)° , we substitute these expressions into the equation:

(5x - 22) + (x + 28) = 180

Combine like terms:

6x + 6 = 180

Subtract 6 from both sides:

6x = 174

Divide by 6:

x = 29

Now that we have the value of
`\( x \)`, we can find the measure of ∠1:

m∠1 = 5x - 22 = 5(29) - 22 = 145 - 22 = 123°