Question

In RST, RU≅US and RV≅VT, If UV, the midsegment, is equal to 2x - 2 and

ST = 8x - 28, find the value of x. Show all work for credit.

Answer 1

Check the picture below.

`\stackrel{m}{2x-2}~~ = ~~\cfrac{\stackrel{base}{8x-28}}{2}\implies 4x-4=8x-28\implies -4=4x-28 \\\\\\ 24=4x\implies \cfrac{24}{4}=x\implies 6=x`

Answer 2

x = 6

Explanation:

Given:

In RST, RU≅US and RV≅VT

UV the mid-segment, is equal to 2x - 2 and ST = 8x - 28

To find:

value of x

Solution:

Since In triangle RST, UV is the mid-segment, so it is parallel to ST. This means that the triangle UVT is similar to the triangle RST.

Note:

A mid-segment of a triangle is a line segment that connects the midpoints of two sides of the triangle. A mid-segment is parallel to the third side of the triangle and is half as long as the third side.

This means that:

`\sf UV = (ST)/(2)`

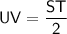
Substitute the value of UV and ST, we get

`\sf 2x - 2 = (8x - 28)/(2)`

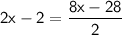
Multiplying both sides by 2, we get:

`\sf 2(2x - 2)= (8x - 28)/(2)* 2`

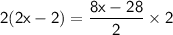
Simplify:

`\sf 4x - 4 = 8x - 28`

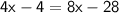
Subtracting 4x from both sides, we get:

`\sf 4x - 4 -4x= 8x - 28 - 4x`

`\sf -4 = 4x - 28`

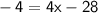
Adding 28 to both sides, we get:

`\sf -4 +28= 4x - 28+28`

`\sf 24 = 4x`

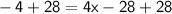
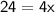
Dividing both sides by 4, we get:

`\sf ( 24 )/(4) = (4x)/(4)`

`\sf x = 6`

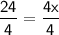
Therefore, the value of x is 6.