Question

Solve the literal equation a(bx+c)=d

for x
. State any necessary restrictions on the letters representing constants in the equation. Then use the solution of the literal equation to solve −3(2x+1)=4
.

Answer 1

`x=(d-ac)/(ab) \ \text{and} \ x= -(7)/(6)`

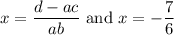
Explanation:

To solve the given literal equation for 'x', we will distribute the terms, isolate 'x' on one side of the equation, and then specify any restrictions on the constants. Subsequently, we'll use this solution to solve the given equation.

Given:

`\bullet \ a(bx+c)=d \\ \\ \bullet \ -3(2x+1)=4`

`\hrulefill`

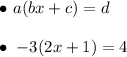
Solving the given literal equation for 'x':

We have,

`\Longrightarrow a(bx+c)=d`

Distribute 'a':

`\Longrightarrow abx+ac=d`

Isolate 'x':

`\Longrightarrow abx=d-ac\\\\\\\\\therefore \boxed{x=(d-ac)/(ab)}`

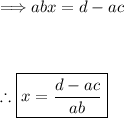
Restrictions on the letters:

For any fraction, the denominator cannot be zero. So, 'ab' cannot be zero, which implies:

• 'a' cannot be zero.

• 'b' cannot be zero.

`\hrulefill`

Use the solution above to solve the given equation:

We have,

`\Longrightarrow -3(2x+1)=4; \ \text{where} \ a=-3, \ b=2, \ c=1, \text{and} \ d=4`

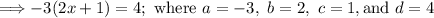
Plug these values into the solution found above:

`\Longrightarrow x=(d-ac)/(ab)\\\\\\\\\Longrightarrow x=(4-(-3)(1))/((-3)(2))`

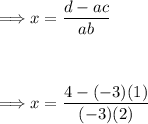
Simplify the fraction:

`\Longrightarrow x= (4+3)/(-6)\\\\\\\\\therefore \boxed{x= -(7)/(6)}`

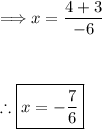
Thus, the problem is solved.