Question

I need help with problem 18

Answer 1

Domain of f(x): [3, ∞)

Range of f(x): (-∞, 0]

f⁻¹(x) = x² + 3

Domain of f⁻¹(x): (-∞, 0]

Explanation:

Given square root function:

`f(x) = -√(x-3)`

The domain of a function is the set of all possible input values (x-values) for which the function is defined.

A square root is only defined for non-negative values. Therefore, to find the domain of f(x), set the expression under the square root sign to greater than or equal to zero, then solve the inequality for x:

`x - 3 \geq 0 \implies x \geq 3`

Therefore, the domain of function f(x) is [3, ∞).

The range of a function is the set of all possible output values (y-values) for which the function is defined.

Since a negative sign precedes the square root in function f(x), the range is constrained to values that are less than or equal to zero. Therefore, the range of function f(x) is (-∞, 0].

To find the inverse of the function, begin by switching the x and y:

`x = -√(y-3)`

Now, rearrange the equation to isolate y:

`\begin{aligned}(x)/(-1) &= (-√(y-3))/(-1)\\\\-x &= √(y-3)\\\\(-x)^2 &= (√(y-3))^2\\\\x^2&=y-3\\\\y&=x^2+3\end{aligned}`

Replace y with f⁻¹(x):

`f^(-1)(x)=x^2+3`

The domain of the inverse of a function is the same as the range of the original function. Therefore, since the range of f(x) is limited to (-∞, 0], then it follows that the domain of the inverse function is also restricted to (-∞, 0].

Additional Notes

The inverse of a function is a reflection of the original function across the line y = x. If we do not limit the domain of the inverse function f⁻¹(x), it would not be a reflection of the original function in this line.

Answer 2

Domain of f(x): x ≥ 3 or [3, ∞)

Range of f(x): y ≥ 0 or (-∞, 0]

Inverse of f(x):
`f^(-1)(x) = -x^2 + 3`

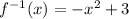
Domain of
`f^(-1)(x)`: x ∈ ℝ or (-∞, ∞)

Explanation:

We are given the function:

`f(x) = -√(x-3)`

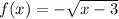
and asked to find its domain and range as well as the domain of its inverse function.

First, we can find
`f(x)`'s domain by using our knowledge of the square root function. We know that it only returns a real value when the value inside of it is positive or zero. Therefore, to solve for the function's domain, we can set the expression under the square root greater than or equal to 0 and solve for x:

`x - 3 \ge 0`

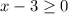
+ 3 + 3

`\boxed{x \ge 3}`

So, the domain of
`f(x)` is x ≥ 3, or [3, ∞) in interval notation.

To find the range of
`f(x)`, we can examine the behavior of the function from the leftmost area of its domain; we can plug in certain values for x around x = 3 and find the corresponding function output. Additionally, we can use our knowledge of the square root function to hypothesize what will happen as x approaches infinity:

`\begin{array}\cline{1-2} x & f(x) \\ \cline{1-2} 3 & 0 \\ \cline{1-2}7 & -2 \\ \cline{1-2} 12 & -3 \\ \cline{1-2} 19 & -4\\ \cline{1-2}\end{array}`

We can see that
`f(x)`, which we call
`y` in the context of range, extends from 0 to negative infinity. Therefore, the range of the function is:

x ≤ 0 or (-∞, 0]

______________

Next, we can find the inverse of
`f(x)`:
`f^(-1)(x)`.

The operations done onto x in the original function are:

1. subtract 3
2. square root
3. multiply by -1

So, the operations for the inverse function will be:

1. divide by -1
2. square
3. add 3

Notice how we inverted the order of each operation's opposite.

In equation form, this is:

`f^(-1)(x) = -x^2 + 3`

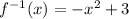
The inverse function's domain is all real numbers because there are no restricting operations (like square root) in it:

x ∈ ℝ or (-∞, ∞)