Question

Hi anyone know hw to do this question?​

Answer 1

∠EOG = 2.322 radians

Explanation:

The diagram shows a semicircle EGF with its center at O and a diameter measuring 8.6 cm. Point G lies on the curved section of the semicircle. Since the diameter of a circle is twice its radius, the radii of the semicircle (OE, OF, and OG) each measure 4.3 cm.

To find the measure of ∠EOG, first find the measure of ∠FOG.

Given the length of arc FG is 3.526 cm, we can use the arc length formula to find the measure of angle ∠FOG.

`\boxed{\begin{array}{l}\underline{\sf Arc\; length}\\\\\textsf{Arc length $=r\theta$}\\\\\textsf{where:}\\\phantom{ww}\;\bullet\;\textsf{$r$ is the radius.}\\ \phantom{ww}\;\bullet\;\textsf{$\theta$ is the central angle measured in radians.}\\\end{array}}`

In this case:

• Arc length = 3.526 cm
• r = 4.3 cm
• θ = ∠FOG

Substitute the values into the formula and solve for ∠FOG:

`3.526=4.3\cdot \angle FOG`

`\angle FOG=(3.526)/(4.3)`

`\angle FOG=0.82\; \sf rad`

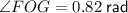
Angles on a straight line sum to π radians. Therefore, to find the measure of ∠EOG, simplify subtract the found measure of ∠FOG from π:

`\angle EOG = \pi-\angle FOG`

`\angle EOG = \pi-0.82`

`\angle EOG = 2.322\; \sf rad\;(3\;d.p.)`

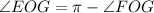
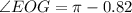
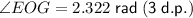
Therefore, the measure of ∠EOG is 2.322 radians (rounded to 3 decimal places).