Answer:
Length of track = 357.08 m
Area enclosed by the track = 6,963.50 m²
Explanation:
An oval track is made by erecting semicircles on each end of a 50 m by 100 m rectangle. Since the diameter (d) of these semicircles is equal to the width of the track (50 m), we have d = 50 m.
The total length of the track is obtained by summing the lengths of the two longer edges of the rectangle (100 m each) and the curved portions of the circumferences of the two semicircles. As the sum of two semicircles forms a complete circle, and the circumference of a circle is calculated as πd, we get:
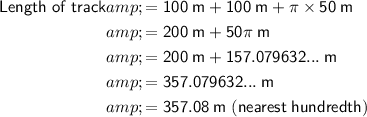
Therefore, the length of the track is 357.08 m.
The area of a rectangle is the product of its width and length. The formula for the area of a circle is πr², where 'r' represents the radius. Since the radius is half the diameter, and the diameter of the semicircles is 50 m, then the radius of each semicircle is 25 m. Therefore, the area enclosed by the track is:

Therefore, the area enclosed by the track is 6,963.50 m².