Question

A 1.00 g sample of an unknown gas has a pressure of 35.8 mmHg a volume of 20.0 Land a temperature of 25 C. what is the molar mass of the gas? Use the ideal gas law to calculate number of moles. Molar mass is mass of 1 mole ( R= 0.0821 atm L/mol K)

Answer 1

To find the molar mass of an unknown gas using the ideal gas law, convert the temperature to Kelvins and the pressure to atm, then calculate the number of moles with PV = nRT and divide the mass of the gas by the number of moles.

Step-by-step explanation:

To calculate the molar mass of an unknown gas using the ideal gas law, we can apply the formula PV = nRT, where P is the pressure, V is the volume, n is the number of moles, R is the universal gas constant, and T is the temperature in Kelvins. First, we need to convert the given temperature to Kelvins by adding 273.15 to the Celsius temperature, and convert the pressure from mmHg to atm (1 atm = 760 mmHg) for use with the value of R given in atm L/mol K.

Convert the temperature: 25 °C + 273.15 = 298.15 K
Convert the pressure: 35.8 mmHg ÷ 760 mmHg/atm = 0.0471 atm

Next, we plug in the values into the ideal gas law to calculate the number of moles (n):

0.0471 atm × 20.0 L = n × 0.0821 atm L/mol K × 298.15 K

Solving for n gives:
n = (0.0471 atm × 20.0 L) / (0.0821 atm L/mol K × 298.15 K)

The molar mass (M) can then be calculated by dividing the mass of the gas sample by the number of moles:
M = 1.00 g / n.
Use the value of n from the previous calculation to find the molar mass of the unknown gas.

Answer 2

Molar mass is mass of 1 mole is approximately 25.98 grams

To determine the molar mass of the unknown gas, we'll follow these steps:

1. Convert Given Units to Appropriate Units for Ideal Gas Law

- Pressure: Convert from mmHg to atm (1 atm = 760 mmHg).

- Volume: Given in liters (L), which is appropriate.

- Temperature: Convert from Celsius to Kelvin (K = C + 273.15).

2. Use the Ideal Gas Law

The ideal gas law is given by PV = nRT , where:

- P is pressure in atm,

- V is volume in liters,

- n is the number of moles,

- R is the gas constant (0.0821 atm L/mol K),

- T is temperature in Kelvin.

3. Calculate the Number of Moles n

Rearrange the ideal gas law to solve for
`\( n \): \( n = (PV)/(RT) \).`

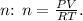
4. Calculate Molar Mass

Molar mass is the mass of 1 mole of the substance. It is given by:

`\[ \text{Molar Mass} = \frac{\text{Mass of the sample}}{n} \]`

Step-by-Step Calculations

Convert Units

- Pressure:

`\( P = 35.8 \, \text{mmHg} * \frac{1 \, \text{atm}}{760 \, \text{mmHg}} \)`

- Temperature:

T=25°C+273.15

Let's perform these conversions and then calculate the number of moles.

With the converted units, the pressure is approximately 0.0471 atm, and the temperature is 298.15 K.

5. Calculate the Molar Mass of the Gas

Now, using the calculated number of moles (0.0385 moles) and the given mass of the sample (1.00 g), the molar mass of the gas can be calculated as follows:

`\[ \text{Molar Mass} = \frac{\text{Mass of the sample}}{n} = \frac{1.00 \, \text{g}}{0.0385 \, \text{moles}} \]`

Let's calculate the molar mass

The molar mass of the unknown gas is approximately 25.98 grams per mole.