Question

Gcse question 6 marker

Answer 1

£107.95

Explanation:

We can use a system of equations to solve this problem, with the following variables:

• A: The number of hours Amir worked.
• B: The number of hours Beth worked.
• C: The number of hours Charlie worked.

We are given the following information:

• B = 2A
• C = A + 5
• A + B + C = 85

We can substitute the first two equations into the third equation to get:

A + (2A) + (A + 5) = 85

Combining like terms, we get:

4A + 5 = 85

Subtracting 5 from both sides, we get:

4A + 5 - 5 = 85 - 5

4A = 80

Dividing both sides by 4, we get:

`\sf (4A )/(4)= (80)/(4)`

A = 20

Now that we know A, we can find B and C using the equations B = 2A and C = A + 5:

B = 2A = 2 × 20 = 40

C = A + 5 = 20 + 5 = 25

We are also given that Amir's share of the tips was £25.40. Let T be the total amount of tips received.

The ratio of the tips received by Amir, Beth, and Charlie is:

Amir:Beth:Charlie = A:B:C = 20:40:25 also 4:8:5

We can use this ratio to set up a proportion to find T:

`\sf (4)/(17) T = £ 25.40`

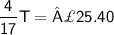
Multiplying both sides by
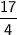`\sf (17)/(4)`, we get

`\sf T = £ 25.40 * (85 )/(20)`

`\sf T = £107.95`

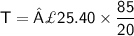
Therefore, the total amount of tips received this week was £107.95.

Answer 2

£107.95

Explanation:

To calculate the total amount of tips received that week, we can first set up a system of equations based on the given information to determine how many hours Amir worked that week.

Definition of variables:

• Let x be the number of hours Amir worked.
• Let y be the number of hours Beth worked.
• Let z be the number of hours Charlie worked.

Given that Beth worked twice as many hours as Amir:

`y = 2x`

Given that Charlie worked 5 more hours than Amir:

`z = x + 5`

Given that the total hours worked by Amir, Beth and Charlie was 85 hours:

`x+y+z=85`

Therefore, we have the following system of equations:

`\begin{cases}y = 2x\\z = x + 5\\x+y+z=85\end{cases}`

Substitute the first and second equations into the third equation, then solve for x:

`\begin{aligned}x+2x+x+5&=85\\\\4x+5&=85\\\\4x+5-5&=85-5\\\\4x&=80\\\\(4x)/(4)&=(80)/(4)\\\\x&=20\end{aligned}`

Therefore, since x = 20, the number of hours Amir worked was 20 hours.

We know that Amir's share of the tips is £25.40, so we can calculate the rate of the tips per hour by dividing £25.40 by the number of hours Amir worked:

`\textsf{Tips}=(\£25.40)/(20\; \sf hours)=\£1.27\;\sf per\;hour`

Given that the total hours worked by the three employees was 85 hours, to calculate the total amount of tips received, simply multiply the rate by 85 hours:

`\begin{aligned}\textsf{Total tips}&=\sf \£1.27\; per\;hour * 85 \;hours\\\\&=\sf \£107.95\end{aligned}`

Therefore, the total amount of tips received was £107.95.