Question

Using the general energy equation for the motion of the package between the initial and the lowest point, find the distance that the spring is compressed when the package is at its lowest point. Express your answer with the appropriate units.

Answer 1

The diver's moment of inertia in the tuck position is found to be 0.6 kg·m^2 using the conservation of angular momentum, given that no external torque acts on him.

Step-by-step explanation:

The question relates to the concept of conservation of angular momentum, which is a principle in physics stating that if no external torque acts on a system, the total angular momentum of the system remains constant. In this problem, a diver's angular velocity increases as he changes from a relaxed position to a tucked position, indicating that his moment of inertia must decrease to conserve angular momentum because external torque is zero.

To solve for the diver's moment of inertia in the tucked position, we use the formula for conservation of angular momentum:

1. L_initial = L_final
2. I_initial * ω_initial = I_final * ω_final
3. (1.2 kg·m2) * (6.0 rad/s) = I_final * (12 rad/s)
4. I_final = (1.2 kg·m2 * 6.0 rad/s) / 12 rad/s
5. I_final = 0.6 kg·m2

Therefore, the moment of inertia of the diver in the tuck position is 0.6 kg·m2.

Answer 2

The maximum compression of the spring is
`\( 2.088 \, \text{m} \)`.

How to determine the maximum compression of the spring?

Given the general energy equation between state 1 and 2:

`\[ \mu - z = (x + D) \cdot \sin(\theta) \]`

Where:

`\( x \)` → maximum compression of the spring

`\( D = 5 \, \text{m} \)`

`\( m = 6 \, \text{kg} \)\( R = 130 \, \text{N/m} \)`

`\( \theta = 53.1^\circ \)\( \mu_R = 0.2 \)`

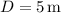
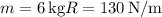
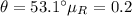
From the energy equation between state 1 and 2:

`\[ mg\mu = mgz \, (\text{block energy}) + (1)/(2)Rx^2 \, (\text{spring energy}) + \mu mg \cos(\theta) * (D + x) \,`
`(\text{energy loss due to friction})`

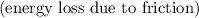
Therefore:

`\[ mg \cdot (\mu - 2) = (1)/(2)Rx^2 + \mu mg \cdot (D+x) \cdot \cos(\theta) \]`

`\[ mg \cdot (x+D) \cdot \sin(\theta) = (1)/(2)Rx^2 + \mu mg \cdot (D+x) \cdot \cos(\theta) \]`

`\[ mg \cdot (x + D) \cdot (\sin(\theta) - \mu \cos(\theta)) = (1)/(2)Rx^2 \]`

Substituting the given values:

`\[ 6 * 9.81 * (x+5) * [\sin(53.1) - 0.2 * \cos(53.1)] = (1)/(2) * 130 * x^2 \]`

`\[ x+5 = 1.625x^2 \]`

Solving the equation yields:

`\[ x = 2.088 \, \text{m} \]`

Hence, the maximum compression of the spring is
`\( 2.088 \, \text{m} \)`.

See image below for missing part of the question.