Question

You are the manager of a Mom and Pop store that can buy milk from a supplier at $3.00 per gallon. If you believe the elasticity of demand for milk by customers at your store is −4, then your profit-maximizing price is: A) $5.00 B) $6.00 C) $7.00 D) $8.00

Answer 1

The profit-maximizing price would be $4.00 per gallon based on the demand elasticity of −4 and the cost of $3.00 per gallon; however, this price is not listed among the choices ($5.00, $6.00, $7.00, $8.00). There might be a typo in the question or provided choices.

Step-by-step explanation:

You are the manager of a Mom and Pop store and are considering the profit-maximizing price for milk, given that the elasticity of demand for milk is −4 and the supplier's price is $3.00 per gallon. The elasticity of demand signifies how much the quantity demanded will change in response to a change in price. In this case, a highly elastic demand with an elasticity of −4 implies that the quantity demanded is very sensitive to price changes. According to the price elasticity formula, the optimal markup on cost can be calculated as (1/(1 + elasticity)). Substituting in the given elasticity, the formula becomes (1/(1 - 4)), which simplifies to −1/3. Therefore, the markup on cost is −1/3 of the cost price, which is $3.00 per gallon. Multiplying −1/3 by $3.00 gives a markup of $1.00, hence the profit-maximizing price is $3.00 (cost) + $1.00 (markup) = $4.00 per gallon. However, this price is not one of your provided choices. If you are limited to the choices given ($5.00, $6.00, $7.00, $8.00), the correct answer is actually not listed. If we've made an error and the elasticity of demand is positive 4 instead of negative (since elasticity is typically expressed as a negative number due to the inverse relationship between price and quantity demanded), the calculation would change accordingly, and then the profit-maximizing price would be one of the choices provided. Given the information and typical elasticity values, there might be a typo or misunderstanding in the question or choices provided.

Answer 2

Based on the given information, the profit-maximizing price is $4.00.

The profit-maximizing price is a dynamic concept influenced by both cost considerations and the responsiveness of consumer demand. Elasticity of demand plays a crucial role in guiding businesses toward setting prices that align with market dynamics and maximize overall profitability.

To find the profit-maximizing price, we can use the formula for the optimal price when considering elasticity of demand:

`P_{\text {optimal }}=\frac{M C}{1+\frac{1}{\text { Elasticity of Demand }}}`

Where:

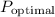`P_{\text {optimal }}` is the profit-maximizing price.

MC is the marginal cost.

Elasticity of Demand = −4 (negative because it's elastic).

Given:

MC = $3.00 (cost per gallon from the supplier).

Elasticity of Demand = −4.

Substituting these values into the formula:

`P_{\text {optimal }}=(\$ 3.00)/(1+(1)/(-4))`

`P_{\text {optimal }}=(\$ 3.00)/(1-(1)/(4))`

`P_{\text {optimal }}=(\$ 3.00)/((3)/(4))`

`P_{\text {optimal }}=\$ 4.00`

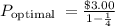
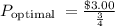
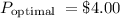
So, $4.00 is the profit-maximizing price. Thus, option B is the correct answer.

Correct Question:

You are the manager of a Mom and Pop store that can buy milk from a supplier at $3.00 per gallon. If you believe the elasticity of demand for milk by customers at your store is -4, then your profit-maximizing price is

A. $2.50.

B. $4.00.

C. $2.00.

D. $5.00.