Question

Find the points on the ellipse 3x^2 + y^2 = 3 that are farthest away from the point (1, 0). Smaller y-value (x, y) = larger y-value. Option 1: (-1, 1) Option 2: (-1, -1) Option 3: (1, 1) Option 4: (1, -1)

Answer 1

To find the points on the ellipse
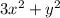`3x^2 + y^2`= 3 that are farthest away from the point (1, 0), we can use the formula for the distance between two points on the plane and maximize it using Lagrange multipliers. The farthest points on the ellipse are (-1, 1) and (1, -1).

Step-by-step explanation:

To find the points on the ellipse
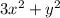`3x^2 + y^2` = 3 that are farthest away from the point (1, 0), we can use the formula for the distance between two points on the plane. Let's call the point on the ellipse (x, y). The distance between (x, y) and (1, 0) is given by:

d = sqrt(
`(x - 1)^2 + y^2)`

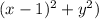
Since we want to find the point (x, y) that maximizes the distance d, we can maximize the expression
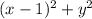`(x - 1)^2 + y^2`, subject to the constraint
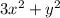`3x^2 + y^2` = 3. This can be done using Lagrange multipliers. By solving the system of equations:

2(x - 1) = λ(6x)

2y = λ(2y)

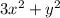`3x^2 + y^2` = 3

We can find the values of x and y that correspond to the farthest points on the ellipse from (1, 0). After solving the system, we find that the points (-1, 1) and (1, -1) are the farthest points on the ellipse from (1, 0).