Question

A wire length 28 pi inch is bent to form a circle what is the radius of the circle​

Answer 1

>>> 14 inch

Explanation:

Given ,

• Length of wire that is 28π inch which is bent in form of circle

We have to find ,

• Radius of circle

Solution :

According to Question , a wire of length 28π inch is beng to form a circle which means we are provided with the circumference of circle that is 28π.

For finding the radius of circle we are comparing given circumference i.e. 28π with the circumference of circle i.e. 2πr

`\: \: \: \: \: \: \: \: \: \: \: \boxed{ \sf{Circumference_((Circle)) = 2 \pi r} }`

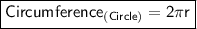
Where ,

• r refers to radius of circle

• π can be 22/7 or 3.14

`\dashrightarrow \: \: \: \sf{2 \cancel{\pi }r = 28 \cancel{\pi}}`

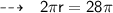
After cancelling π , we have ,

`\dashrightarrow \: \: \: \sf{2 r = 28 }`

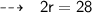
Dividing both sides with 2 :

`\dashrightarrow \: \: \: \sf{ \frac{ \cancel{2 } r }{ \cancel{2}}= \cancel{ (28 )/(2)}}`

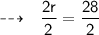
We get ,

`\dashrightarrow \: \: \: \underline{ \boxed{ \sf{ \bold{r = 14 \:inch}}}} \: \: \: \bigstar`

• Therefore, radius of circle is "14 inch"

Answer 2

• 14 inch

Given :

• circumference = 28π inch

To find :

• radius

Solution :

we know that,

• circumference = 2πr
• 28π inch = 2πr
• r = 28π inch/2π
• r = 14 inch

Thus, our radius would be equal to 14 inches.

`\:`