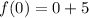Answer:
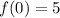
Explanation:
In this problem we are given the piecewise function:
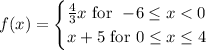
and are asked to calculate
 .
.
First, we can identify which piece will determine the output for
 . We can see that it will be the piece:
. We can see that it will be the piece:
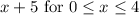
because
 is within its domain (possible inputs, or x-values).
is within its domain (possible inputs, or x-values).
Notice that the other piece's domain is less than 0, but does not include 0.
Next, we can plug
 in for
in for
 within that piece's definition to solve for
within that piece's definition to solve for
 :
: