Answer and Explanation:
We can determine if the piecewise function:
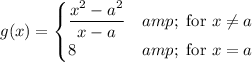
is continuous for all values of x by looking at the following conditions:
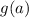 is defined
is defined
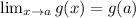
To evaluate the first condition, we can look to which piece of the function operates on the domain including
 . We can see that this piece is:
. We can see that this piece is:

Therefore, the first condition is satisfied.
To evaluate the second condition, we can take take the limit of the other piece of the function as x approaches a, and make sure that it approaches the actual value of
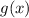 at x = a, which is 8.
at x = a, which is 8.
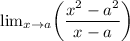
↓ factoring the numerator within the limit
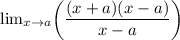
↓ canceling the common term in the numerator and denominator (x - a) to fill in the removable discontinuity
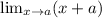
↓ evaluating the limit

↓ executing the addition
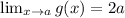
Now, we can compare this to the actual value of
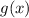 at x = a:
at x = a:
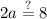
↓ dividing both sides by 2
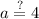
Finally, we can see that the function is only continuous for all values of x if
 .
.