Question

If we are asked how many 5 digit lock codes we can make, are we dealing with permutations or combinations?

Answer 1

Permutations

Explanation:

We are dealing with permutations because the order of the digits matters. For example, 12345 and 54321 are different lock codes.

Here's why:

• Permutations: The order of the items matters.
• Combinations: The order of the items does not matter.

In the case of a 5-digit lock code, the order of the digits matters because each digit represents a different position on the lock. If we enter the digits in the wrong order, the lock will not open.

To calculate the number of possible permutations for a 5-digit lock code, we can use the following formula:

`\sf (n!)/((n-r)!)`

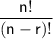
where:

n is the total number of items (in this case, 10 digits)

r is the number of items we are selecting (in this case, 5 digits)

So, the number of possible permutations for a 5-digit lock code is:

`\sf (10! )/( (10-5)! )=(10!)/(6!) =(10* 9* 8* 7* 6!)/(6!)= 30,240`

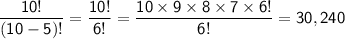
This means that there are 30,240 possible lock codes for a 5-digit lock.