Question

Find d, the horizontal distance between the centers of the two circles.

If someone could guide me through this I'd appreciate it.

Answer 1

11.856

Explanation:

Draw radial lines from the center of each circle to the tangent points. The result will be two kites: a left one with a base angle of 90° (a square), and a right one with a base angle of 60°.

Next, draw lines from the base of the kites to the center of each circle. This cuts each kite in half.

On the right, there is a 30-60-90 triangle with a short side of 6, which means the long side is 6√3. So the x-coordinate of the right circle's center is 6√3 ≈ 10.392.

On the left, there is a 45-45-90 triangle with short side 4, which means the hypotenuse is 4√2. The hypotenuse is rotated at an angle of 60° + 45° = 105° relative to the +x axis. So the x-coordinate of the left circle's center is 4√2 cos 105° ≈ -1.464.

The distance between the centers is therefore:

10.392 − -1.464 ≈ 11.856

Answer 2

d = 11.856 (3 d.p.)

Explanation:

A tangent is a straight line that touches a circle at only one point. Tangents drawn from a common point to a circle are always equal in length, and theses tangents are always perpendicular to the radius.

Larger circle (diameter = 12 units)

These properties imply that if we connect the center of the larger circle to the two points of tangency, we form a kite where its opposite congruent angles are right angles. Consequently, drawing a line from the circle's center to the opposite vertex of the kite creates two congruent right triangles. As the angle between the two longest sides of the kite is 60°, then the angle at the vertex of these right triangles is 30°. Therefore, we have two congruent 30-60-90 right triangles, with the shortest leg measuring 6 units. Since the side lengths of such a triangle follow the ratio 1 : √3 : 2, the length of the longest leg is 6√3 units.

Smaller circle (diameter = 8 units)

From observation of the diagram, the angle at the vertex where the two tangent lines meet outside the smaller circle is 90°. Since tangents to a circle are always perpendicular to its radius, the shape formed by the tangent segments and the radii of the smaller circle is a square with side lengths measuring 4 units.

The diagonal of a square is given by s√2, where s represents the side length. Therefore, the line drawn from the center of the circle to the exterior point where the two tangent lines meet measures 4√2 units.

By drawing a vertical line from the center of this circle, we create a right triangle (shaded in green on the attached diagram) with a hypotenuse of 4√2 units. By observation, the length of the longest leg of this triangle is 5.464 units. To determine the shortest leg of this triangle, we can apply the Pythagorean Theorem:

`\sqrt{(4√(2))^2-5.464^2}=1.464\; \sf (3\;d.p.)`

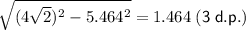
So, the shortest leg of the green right triangle is 1.464 units (3 d.p.).

The distance (d) between the centers of the two circles is the sum of 6√3 and 1.464:

`d=6√(3)+1.464=11.856\; \sf (3\;d.p.)`

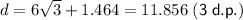
Therefore, d = 11.856 (3 d.p.).