Question

I've tried to solve this for 2 hours please help. 100 points!

Name any x-intercepts and y-intercepts of the function.
Name the coordinates of any holes of the function.
State the equations of any asymptotes of the function.

Answer 1

`\textsf{$x$-intercept} = (0, 0)`

`\textsf{$y$-intercept} = (0, 0)`

`\textsf{Vertical asymptote:}\quad x = -(3)/(2)`

`\textsf{Horizontal asymptote:}\quad y = (1)/(2)`

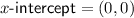
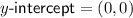
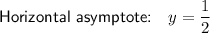
Explanation:

Given rational function:

`f(x)=(x^2-3x)/(2x^2-3x-9)`

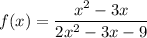
Begin by factoring the numerator and the denominator.

For the numerator, factor out the common term x:

`x^2-3x=x(x-3)`

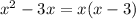
For the denominator, split the middle term and factor:

`\begin{aligned}2x^2-3x-9&=2x^2-6x+3x-9\\&=2x(x-3)+3(x-3)\\&=(2x+3)(x-3)\end{aligned}`

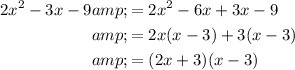
Therefore the factored form of the function is:

`f(x)=(x(x-3))/((2x+3)(x-3))`

Cancel the common factor (x - 3):

`f(x)=(x)/(2x+3)`

`\hrulefill`

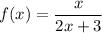
x-intercept

The x-intercepts are the points at which the curve crosses the x-axis, so when y = 0. Therefore, to find the x-intercepts, set the simplified function to zero and solve for x:

`\begin{aligned}(x)/(2x+3)&=0\\\\x&=0\end{aligned}`

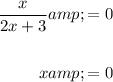
So, the x-intercept is the origin (0, 0).

`\hrulefill`

y-intercept

The y-intercept is the point at which the curve crosses the y-axis, so when x = 0. Therefore, to find the y-intercept, substitute x = 0 into the simplified function:

`f(0)=(0)/(2(0)+3)=(0)/(3)=0`

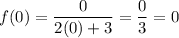
Therefore, the y-intercept is the origin (0, 0).

`\hrulefill`

Removable discontinuity (hole)

When a rational function has a factor with an x that is in both the numerator and the denominator, it is called a removable discontinuity or a "hole".

From the factored form, we can see that (x - 3) is a common factor in both the numerator and the denominator. Therefore, there is a hole at x = 3.

To find the y-coordinate of the hole, substitute x = 3 into the simplified function:

`f(3)=(3)/(2(3)+3)=(3)/(9)=(1)/(3)`

So, there is a hole at (3, 1/3).

`\hrulefill`

Asymptotes

An asymptote is a line that the curve gets infinitely close to, but never touches.

A vertical asymptote occurs at x-value(s) that make the denominator of a rational function equal to zero. Therefore, to determine the vertical asymptote, set the denominator of the simplified function equal to zero and solve for x:

`\begin{aligned}2x+3&=0\\\\2x&=-3\\\\x&=-(3)/(2)\end{aligned}`

Therefore, there is a vertical asymptote at x = -3/2.

Since the degrees of the numerator and denominator are the same, the horizontal asymptote is the result of dividing the coefficients of the highest degree terms:

`y=(1)/(2)`

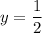
Therefore, there is a horizontal asymptote at y = 1/2.