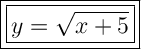Question

Write the equation for the following translations of their particular parent graphs. You may use y= or function

notation (the f(x))

Answer 1

`\textsf{17)}\quad y = x^2 - 5`

`\textsf{18)}\quad y=|x+5|-3`

`\textsf{19)}\quad y=√(x+5)`

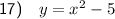
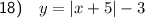
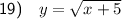
Explanation:

Question 17

The graph shows an upward-opening parabola, indicating that the parent function is y = x².

While the vertex of the parent function is at (0, 0), the graphed function has a vertex at (0, -5). Consequently, the graphed function is the result of a vertical translation of 5 units down. To achieve this translation, we subtract 5 units from the function.

Therefore, the equation of the graphed function is:

`\Large\boxed{\boxed{y = x^2 - 5}}`

`\hrulefill`

Question 18

The graph shows an upward-opening absolute value function, indicating that the parent function is y = |x|.

While the parent function has its vertex at (0, 0), the graphed function's vertex is located at (-3, -5). Therefore, the graphed function is the result of a horizontal translation of 3 units to the left and a vertical translation of 5 units down. When we translate a function n units left, we add n units to the x-value. When we translate a function n units down, we subtract n units from the function.

Therefore, the equation of the graphed function is:

`\Large\boxed{\boxedx+5}`

`\hrulefill`

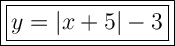
Question 19

The graph shows a square root function, indicating that the parent function is y = √x.

While the parent function begins at the left endpoint (0, 0), the graphed function starts at the left endpoint (-5, 0). Consequently, the graphed function is the result of a translation of 5 units to the left. When we translate a function n units to the left, we add n units to the x-value.

Therefore, the equation of the graphed function is:

`\Large\boxed{\boxed{y=√(x+5)}}`