Question

Find the value of x for which the distance between the points p(4,-5) and q(12,x) is 10 units

Answer 1

To find the value of x for which the distance between the points P(4, -5) and Q(12, x) is 10 units, we can use the distance formula.

The distance formula is given by:

`d = √(((x2 - x1)^2 + (y2 - y1)^2))`

Here, P(4, -5) is our first point with coordinates (x1, y1) and Q(12, x) is our second point with coordinates (x2, y2).

Let's substitute the coordinates into the distance formula:

`10 = √(((12 - 4)^2 + (x - (-5))^2))`

Simplifying the equation:

`10 = \sqrt{8^2 + (x + 5)^2)`

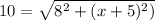
Squaring both sides of the equation:

`100 = 8^2 + (x + 5)^2`

`100 = 64 + (x + 5)^2`

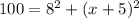
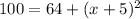
Subtracting 64 from both sides of the equation:

`36 = (x + 5)^2`

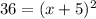
Taking the square root of both sides:

6 = x + 5 or -6 = x + 5

Solving for x, we get two possible values:

`x = 6 - 5 = 1, x = -6 - 5 = -11`

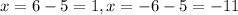
Therefore, the values of x for which the distance between the points P(4, -5) and Q(12, x) is 10 units are x = 1 and x = -11.