Answer:
The resultant of these two forces will be the greatest when the two forces are in the same direction.
Step-by-step explanation:
Let
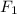 and
and
 denote these two forces. The resultant of these two force would be the vector sum
denote these two forces. The resultant of these two force would be the vector sum
 .
.
Refer to the diagram attached. Join the head of
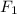 to the tail of
to the tail of
 . Under this construction, the vector connecting the tail of
. Under this construction, the vector connecting the tail of
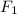 to the head of
to the head of
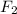 (the vector shown with a lighter color) would represent the resultant vector
(the vector shown with a lighter color) would represent the resultant vector
 .
.
Consider the triangle inequality: as long as
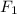 and
and
 (the first two sides of the triangle in the diagram) are not parallel to one another, the magnitude of the resultant vector would always be smaller than the sum of the magnitude of
(the first two sides of the triangle in the diagram) are not parallel to one another, the magnitude of the resultant vector would always be smaller than the sum of the magnitude of
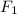 and that of
and that of
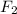 .
.
In other words:
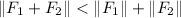 .
.
However, notice that when
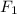 and
and
 are in the same direction, the three sides
are in the same direction, the three sides
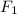 ,
,
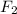 , and
, and
 are in the same line and no longer form a triangle.
are in the same line and no longer form a triangle.
On the other hand, if
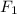 and
and
 are opposite to one another,
are opposite to one another,
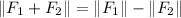 .
.
The magnitudes of the two forces,
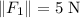 and
and
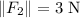 , are fixed. Hence, when the two forces are in the same direction,
, are fixed. Hence, when the two forces are in the same direction,
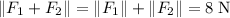 .
.
As long as
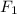 and
and
 are not in the same line, the triangle inequality ensures that
are not in the same line, the triangle inequality ensures that
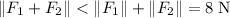 .
.
Hence,
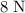 would be the greatest magnitude that the resultant force could achieve. That value is reached when the two forces are in the same direction.
would be the greatest magnitude that the resultant force could achieve. That value is reached when the two forces are in the same direction.