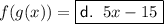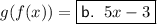Question

Aswer this question thats in the pic

Answer 1

`\textsf{d.}\quad f(g(x))=5x-15`

`\textsf{b.}\quad g(f(x))=5x-3`

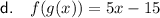
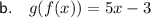
Explanation:

A composite function is when a new function is created by applying one function's output as the input for another function.

In the case of f(g(x)), substitute the output of function g(x) as the input of function f(x). In other words, replace the x-variable of function f(x) with function g(x).

`\begin{aligned}f(g(x))&=f(x-3)\\&=5(x-3)\\&=5x-15\end{aligned}`

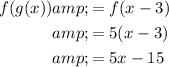
Similarly, to find g(f(x)), replace the x-variable of function g(x) with function f(x):

`\begin{aligned}g(f(x))&=g(5x)\\&=(5x)-3\\&=5x-3\end{aligned}`

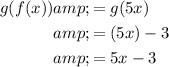
Therefore, the solutions are:

`f(g(x))=\boxed{\textsf{d.}\;\;5x-15}`

`g(f(x))=\boxed{\textsf{b.}\;\;5x-3}`

Answer 2

`\sf f(g(x)) = d.\boxed{5x - 15}`

`\sf g(f(x)) =b.\boxed{ 5x - 3}`

Explanation:

Given:

• f(x) = 5x
• g(x) = x - 3

To find:

• f(g(x))
• g((f(x))

Solution:

To find f(g(x)), we need to substitute g(x) into f(x).

f(g(x)) = f(x - 3)

Now, substitute x-3 in x of f(x), we get

= 5(x - 3)

Simplify:

= 5x - 15

`\hrulefill`

To find g(f(x)), we need to substitute f(x) into g(x).

g(f(x)) = g(5x)

Now, substitute 5x in x of g(x), we get

= 5x - 3

Therefore,

`\sf f(g(x)) = d.\boxed{5x - 15}`

`\sf g(f(x)) =b.\boxed{ 5x - 3}`