Question

Given the interval 0<θ<π/2. Find the angle θ which is formed by the line y = -2x+4 and y = 3x-3

Show your work as well, thank you!​

Answer 1

Consider two vector-valued functions,

`\vec r(t) = \left\langle t, -2t+4\right\rangle \text{ and } \vec s(t) = \left\langle t, 3t-3\right\rangle`

Differentiate both to get the corresponding tangent/direction vectors:

`(\mathrm d\vec r(t))/(\mathrm dt) = \left\langle1,-2\right\rangle \text{ and } (\mathrm d\vec s(t))/(\mathrm dt) = \left\langle1,3\right\rangle`

Recall the dot product identity: for two vectors
`\vec a` and
`\vec b`, we have

`\vec a \cdot \vec b = \|\vec a\| \|\vec b\| \cos(\theta)`

where
`\theta` is the angle between them.

We have

`\langle1,-2\rangle \cdot \langle1,3\rangle = \|\langle1,-2\rangle\| \|\langle1,3\rangle\| \cos(\theta) \\\\ 1*1 + (-2)*3 = √(1^2 + (-2)^2) * √(1^2+3^2) \cos(\theta) \\\\ \cos(\theta) = (-5)/(\sqrt5*√(10)) = -\frac1{\sqrt2} \\\\ \implies \theta = \cos^(-1)\left(-\frac1{\sqrt2}\right) = \frac{3\pi}4`

Then the acute angle between the lines is π/4.

Answer 2

`\rm\displaystyle \theta = (\pi)/(4)`

Explanation:

we want to find the acute angle θ (as θ is between (0,π/2)) formed by the line y=-2x+4 and y=3x-3 to do so we can consider the following formula:

`\displaystyle\tan( \theta) = \bigg| ( m_(2) - m_(1) )/(1 + m_(1) m_(2) ) \bigg |`

`\rm \displaystyle \implies\theta = \arctan \left( \bigg | ( m_(2) - m_(1) )/(1 + m_(1) m_(2) ) \bigg | \right)`

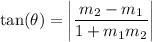
From the first equation we obtain that
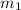`m_1` is -2 and from the second that
`m_2` is 3 therefore substitute:

`\rm\displaystyle \theta = \arctan \left( \bigg | ( 3 - ( - 2) )/(1 + ( - 2) (3)) \bigg | \right)`

simplify multiplication:

`\rm\displaystyle \theta = \arctan \left( \bigg | ( 3 - ( - 2) )/(1 + ( - 6)) \bigg | \right)`

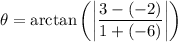
simplify Parentheses:

`\rm\displaystyle \theta = \arctan \left( \bigg | ( 3 + 2 )/(1 + ( - 6)) \bigg | \right)`

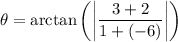
simplify addition:

`\rm\displaystyle \theta = \arctan \left( \bigg | ( 5 )/( - 5) \bigg | \right)`

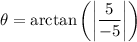
simplify division:

`\rm\displaystyle \theta = \arctan \left( | - 1| \right)`

calculate the absolute of -1:

`\rm\displaystyle \theta = \arctan \left( 1\right)`

calculate the inverse function:

`\rm\displaystyle \theta = (\pi)/(4)`

hence,

the angle θ which is formed by the line y = -2x+4 and y = 3x-3 is π/4

(for more info about the formula refer the attachment thank you!)