Answer:
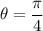
Explanation:
we want to find the acute angle θ (as θ is between (0,π/2)) formed by the line y=-2x+4 and y=3x-3 to do so we can consider the following formula:
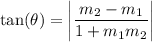
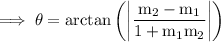
From the first equation we obtain that
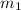 is -2 and from the second that
is -2 and from the second that
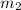 is 3 therefore substitute:
is 3 therefore substitute:
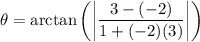
simplify multiplication:
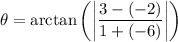
simplify Parentheses:
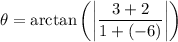
simplify addition:
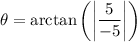
simplify division:
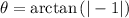
calculate the absolute of -1:
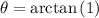
calculate the inverse function:
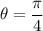
hence,
the angle θ which is formed by the line y = -2x+4 and y = 3x-3 is π/4
(for more info about the formula refer the attachment thank you!)