Question

NO SPAM QUESTIONS IN ATTACHED FILE ​

Answer 1

1) x = 96°

2) y = 24°

3) z = 42°

4) x + 2z = 180°

Explanation:

The diagram displays two intersecting line segments, AB and CD, meeting at point O. Angle COB is divided by line segment EO.

The labeled angles are as follows:

• ∠AOD = 2z
• ∠DOB = x
• ∠BOE = y
• ∠EOC = 60°
• ∠AOC = 4y

According to the Vertical Angles Theorem, when two straight lines intersect, the opposite vertical angles are congruent. Therefore:

`\begin{aligned} m\angle AOC &= m\angle DOB\\4y &= x\end{aligned}`

Additionally:

`\begin{aligned}m\angle AOD &= m\angle BOC\\m\angle AOD &= m\angle BOE + m\angle EOC\\2z &= y + 60^(\circ)\end{aligned}`

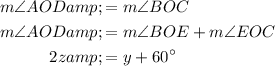
Since angles on a straight line sum to 180°:

`\begin{aligned}m\angle AOC + m\angle AOD &= 180^(\circ)\\4y + 2z &= 180^(\circ)\end{aligned}`

`\begin{aligned}m\angle DOB + m\angle BOE + m\angle EOC &= 180^(\circ)\\x + y + 60^(\circ) &= 180^(\circ)\end{aligned}`

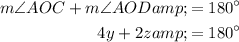
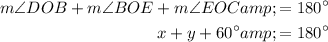
We now have four equations:

• 
  `4y = x`
• 
  `2z = y + 60^(\circ)`
• 
  `4y + 2z = 180^(\circ)`
• 
  `x + y + 60^(\circ) = 180^(\circ)`

Substitute the first equation into the last one and solve for y:

`\begin{aligned}4y + y + 60^(\circ) &= 180^(\circ)\\5y + 60^(\circ) &= 180^(\circ)\\5y &= 120^(\circ)\\y &= 24^(\circ)\end{aligned}`

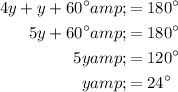
Now, substitute the found value of y into the first equation and solve for x:

`\begin{aligned}4(24^(\circ)) &= x\\x &= 96^(\circ)\end{aligned}`

Substitute the value of y into the second equation and solve for z:

`\begin{aligned}2z &= 24^(\circ) + 60^(\circ)\\2z &= 84^(\circ)\\z &= 42^(\circ)\end{aligned}`

The angles labeled as "x" and "2z" form a linear pair, which means they are two adjacent angles that sum to 180°. Therefore:

`x + 2z = 180^(\circ)`