Question

HELP What is the slope of the line?

Answer 1

`\sf Slope(m)= (1)/(2)`

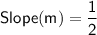
Explanation:

Given:

The points are: (2,1) and (-2,-1)

To find:

Slope

Solution:

The slope of a line is a measure of its steepness. It is calculated as the change in the y-coordinate divided by the change in the x-coordinate.

To find the slope of the line passing through the points (2,1) and (-2,-1), we can use the following formula:

`\sf m = (y_2 - y_1)/( x_2 - x_1)`

where:

m is the slope of the line

(x1, y1) and (x2, y2) are the coordinates of the two points

Substituting the coordinates of the two points into the formula, we get:

`\sf m = (-1 - 1)/(-2 - 2)`

`\sf m = (-2 )/( -4)`

`\sf m = (1)/(2)`

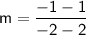
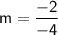
Therefore, the slope of the line passing through the points (2,1) and (-2,-1) is ½.

Answer 2

slope =
`(1)/(2)`

Explanation:

calculate the slope m using the slope formula

m =
`(y_(2)-y_(1) )/(x_(2)-x_(1) )`

let (x₁, y₁ ) = (- 2, - 1) and (x₂, y₂ ) = (2, 1) ← 2 points on the line

substitute these values into the formula for m

m =
`(1-(-1))/(2-(-2))` =
`(1+1)/(2+2)` =
`(2)/(4)` =
`(1)/(2)`