Question

A toy car rolls off the top of a building and attains a vertical velocity of 55 m/s before hitting the ground. How much time did it take the car to fall? a) 5 seconds b) 4 seconds c) 3 seconds d) 2 seconds

Answer 1

Approximately
`5.6\; {\rm s}`, assuming that
`g = 9.81\; {\rm m\cdot s^(-2)}`, the top of the building is level, and that air resistance is negligible.

Step-by-step explanation:

Assume that air resistance on this object is negligible. While in the air, the object would accelerate vertically at a constant rate of
`a = g = 9.81\; {\rm m\cdot s^(-2)}`. In other words, the vertical velocity of this object would increase by
`9.81\; {\rm m\cdot s^(-1)}` for every second that this object in the air.

If the top of the building is level, the object would initially be moving horizontally. The initial vertical velocity of this object would be
`u = 0\; {\rm m\cdot s^(-1)}`.

It is given that during the fall, vertical velocity has increased to
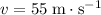`v = 55\; {\rm m\cdot s^(-1)}`. Divide the change in velocity by acceleration (the rate of change of velocity) to find the time taken:

`\begin{aligned} t &= (v - u)/(a) \\ &= \frac{(55\; {\rm m\cdot s^(-1)}) - (0\; {\rm m\cdot s^(-1)})}{(9.81\; {\rm m\cdot s^(-2)})} \\ &\approx 5.6\; {\rm s}\end{aligned}`.

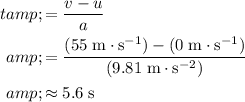In other words, it would have taken approximately
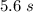`5.6\; {s}` for this object to reach the given velocity.