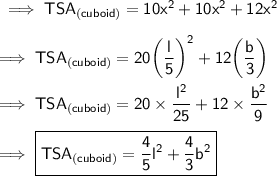
Answer:

Explanation:
A 3D figure is given to us and we need to find the Total Surface area of the 3D figure . So ,
From the cuboid we can see that there are 5 squares in one row on the front face . And there are two rows. So the number of squares on the front face will be 5*2 = 10 .
We know the area of square as ,

Hence the area of 10 squares will be 10x² , where x is the side length of each square. Similarly there are 10 squares at the back . Hence their area will be 10x² .
Also there are in total 12 squares sideways 6 on each sides . So their surface area will be 12x² . Hence the total surface area in terms of side of square will be ,
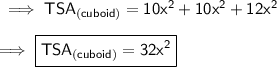
Now let's find out the TSA in terms of side . So here the lenght of the cuboid is equal to the sum of one of the sides of 5 squares .
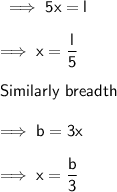

Hence the TSA of cuboid in terms of lenght and breadth is :-