Question

Which off the following is rational number ,√3 ,√4,√5,√6​

Answer 1

`√(4)` = 2

Explanation:

The square root of any number is only rational if that number is a perfect square. Perfect squares include 1 (
`1^(2)`), 4 (
`2^(2)`), 9 (
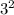`3^(2)`), etc. Basically, you would square each counting number (also known as natural numbers), which are all the numbers from 1 to ∞, to get perfect squares.

Squaring a number is shown through an exponent of 2, which looks like this:
`x^(2)`, where x is a number. When you square a number, you multiply that number by itself. For example,
`5^(2)` = 5 × 5 = 25. Therefore,
`5^(2)` = 25.

When you do the square root of something, shown by a radical (
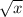`√(x)` where x is a number), you are basically doing the inverse of squaring a number, just like how subtraction is the inverse of addition. Square rooting a number would basically be going backwards. For example,
`√(36)` = 6 because
`6^(2)` = 36. Again, if you square root a number, it will only be rational if that number is a perfect square (1, 4, 9, 16, 25...).

Out of the numbers 3, 4, 5, and 6, only 4 is a perfect square (
`2^(2)` = 4). Thus, the only rational number is
`√(4)`, or just 2.