Question

An aluminium can of mass 100 g contains 200 g of water. Both, initially at 15 °C, are placed in a freezer at -5.0 °C. Calculate the quantity of heat that has to be removed from the water and the can for their temperatures to fall to -5.0 °C. specific heat capacity of aluminium is 0.90 J/(g°c), specific heat capacity of water is 4.20 J/(g °C), specific heat capacity of ice 2.0J/(g°C) and specific latent heat of ice is 340J/g. Select one: a. 84 400 J b. 68 000 J c. 18000 J d. 12 600 J

Answer 1

To calculate the quantity of heat that needs to be removed from the water and the aluminum can for their temperatures to fall to -5.0 °C, we can use the heat transfer equation. The quantity of heat that needs to be removed from the water is -16,800 J and the quantity of heat that needs to be removed from the aluminum can is -1,800 J. The total quantity of heat that needs to be removed is -18,600 J.

Step-by-step explanation:

To calculate the quantity of heat that needs to be removed from the water and the aluminum can for their temperatures to fall to -5.0 °C, we can use the heat transfer equation:

Q = mcΔT

For the water:

1. Mass (m) = 200 g
2. Specific heat capacity (c) = 4.20 J/(g °C)
3. Change in temperature (ΔT) = (-5.0 °C) - (15 °C) = -20 °C

Substituting these values into the equation:

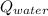`Q_(water)` = (200 g)(4.20 J/(g °C))(-20 °C) = -16,800 J

For the aluminum :

1. Mass (m) = 100 g
2. Specific heat capacity (c) = 0.90 J/(g °C)
3. Change in temperature (ΔT) = (-5.0 °C) - (15 °C) = -20 °C

Substituting these values into the equation:

`Q_(aluminium)` = (100g)(0.90J/(g °C))(-20 °C) = -1,800 J

The total quantity of heat that needs to be removed from the water and the can is the sum of
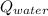`Q_(water)` and
`Q_(aluminium)`:

`Q_(water)` +
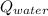`Q_(aluminium)` = -16,800 J + (-1,800 J) = -18,600 J