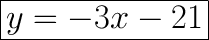Question

Please Help me! Every time x increases by one, y decreases by 3, and when x is -6, y is -3. Which function models the relationship between x and y? A. y = -6x - 21 B. y = -6x - 3 C. y = -3x - 3 D. y = -3x - 21

Answer 1

`\huge\boxed{y = -3x - 21}`

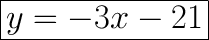
Step-by-step explanation:

We are solving for a linear function (a line), which can be defined by the point-slope form equation:

`y - b = m(x - a)`

where
`m` is the line's slope and
`(a,b)` is a point on the line.

First, we can determine the line's slope (m) using the given information:

• "every time x increases by 1, y decreases by 3"

Therefore, when
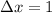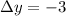`\Delta x = 1` (change in
`x` is 1),
`\Delta y = -3` (change in
`y` is -3).

We know that slope = rise / run, and:

• rise is change in x
• run is change in y

So, the slope of the line is:

`m = -3 / 1`

`\boxed{m = -3}`

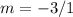
We are also given the information that:

• "when x is -6, y is -3"

Therefore, the line goes through the point
`\boxed{(-6, -3)}`.

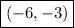Now, we can assign values for the variables in the point-slope form equation:

• 
  `m = -3`
• 
  `a = -6`
• 
  `b=-3`

Finally, we can plug these into the point-slope form equation:

`y - b = m(x - a)`

↓ plugging in the variable values

`y - (-3) = -3(x- (-6))`

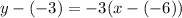
↓ rewriting subtraction of a negative as addition of a positive

`y + 3 = -3(x + 6)`

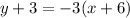
↓ applying the distributive property to the right side ...
`a(b + c) = ab + ac`

`y + 3 = -3x - 18`

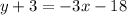
↓ subtracting 3 from both sides

`\huge\boxed{y = -3x - 21}`