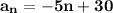Question

Nth term question help please

Answer 1

`\displaystyle{a.) \ \ a_n = -2n+14}\\\\\displaystyle{b.) \ \ a_n = -5n+30}`

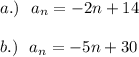
Explanation:

Part A

The common difference is -2 as the sequence decreases down to 2 each. Thus, the sequence is an arithmetic sequence. To find the nth term of an arithmetic sequence, we can follow the formula:

`\displaystyle{a_n = a_1+\left(n-1\right)d}`

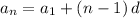
Where
`a_n` is the nth term,
`a_1` is the first term, and
`d` is the common difference which we know that it is -2. By substitution of values we know, we will have:

`\displaystyle{a_n = 12+\left(n-1\right)\left(-2\right)}\\\\\displaystyle{a_n = 12-2n+2}\\\\\displaystyle{a_n = -2n+14}`

Hence, the nth term of the sequence is
`\displaystyle{\bold{a_n = -2n+14}}`

Part B

The common difference is -5 as the sequence decreases by 5 each. This also makes the sequence an arithmetic sequence. Thus, we can apply the same formula as we did previously. By substitution of known values, we will have:

`\displaystyle{a_n = 25+\left(n-1\right)\left(-5\right)}\\\\\displaystyle{a_n = 25-5n+5}\\\\\displaystyle{a_n = -5n+30}`

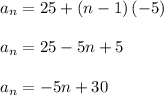
Hence, the nth term of the sequence is
`\displaystyle{\bold{a_n = -5n+30}}`