Question

PLEASE ANSWER AND EXPLAIN THE #3

Answer 1

Problem 1

Answers:

• A ' (-1, -1)
• B ' (3, -1)
• C ' (5, 4)
• Rule:
  `R_(180)(x,y) = (-x,-y)`

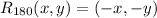
Explanation: You would use the rule mentioned above. Simply negate both x and y coordinates. That means you flip from positive to negative, or vice versa.

========================================================

Problem 2

Answers:

• A ' (2, -2)
• B ' (3, 5)
• C ' (-1, 0)
• Rule:
  `r_(x-axis)(x,y) = (x, -y)`

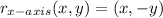
Explanation: When reflecting over the x axis, you flip the y coordinate from positive to negative, or vice versa. The x coordinate stays the same. This means a point like A(2,2) becomes A'(2,-2). Points on the x axis do not move.

========================================================

Problem 3

Part (a)

Answer: 24y-17

Work Shown:

f(x) = 8x-9

f(3y-1) = 8(3y-1)-9 .... replace every x with (3y-1)

f(3y-1) = 24y-8-9

f(3y-1) = 24y-17

-------------------------------

Part (b)

Answer: x = -7/4

Work Shown:

f(x) = -23

8x-9 = -23 .... replace f(x) with 8x-9

8x = -23+9

8x = -14

x = -14/8

x = (-2*7)/(2*4)

x = -7/4