Answer:
As t increases, the quantity reduces
Explanation:
Given
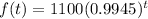
Required
What does the rate (0.9945) reveal about the function
From the given function, the rate b is:

When b has the following range:
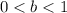
Then, it means there is a reduction
In other words, as the number of weeks (t) increases, the quantity (f(t)) reduces