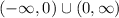Answer:

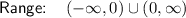
Explanation:
The domain of a function is the set of all possible input values (x-values) for which the function is defined.
The range of a function is the set of all possible output values (y-values) for which the function is defined.
Given functions:
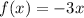
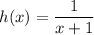
First, determine the composite function (h o f)(x) by substituting function f(x) in place of the x in function h(x):
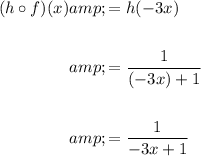
As function (h o f)(x) is a rational function, it is undefined when its denominator equals zero:
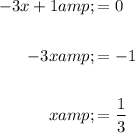
So, the composite function is undefined when x = 1/3.
Therefore, its domain is:

As the degree of the numerator of (h o f)(x) is less than the degree of its denominator, a horizontal asymptote occurs at y = 0. Therefore, the range of the composite function is restricted to: