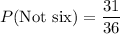Answer:
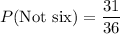
Explanation:
In order to find the probability that the sum of two six-sided dice is not six, we first need to determine the number of outcomes where the sum is not six and then use the formula for probability.
There are 36 possible outcomes when two six-sided dice are rolled.
Now, let's count the outcomes where the sum is not six:
1. Outcomes with a sum of 2: 1 way (1+1)
2. Outcomes with a sum of 3: 2 ways (1+2, 2+1)
3. Outcomes with a sum of 4: 3 ways (1+3, 2+2, 3+1)
4. Outcomes with a sum of 5: 4 ways (1+4, 2+3, 3+2, 4+1)
5. Outcomes with a sum of 7 or more: 21 ways (all other sums)
Now, let's calculate the total number of outcomes where the sum is not six:
Total favorable out
comes = 1 + 2 + 3 + 4 + 21 = 31
The probability of getting a sum that is not six is:
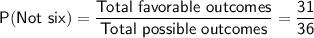
So,
The probability that the sum of two six-sided dice is not six is: