Answer:
See the attached graph.
Explanation:
A piecewise function combines multiple graphs, each representing the function's behavior on a specific interval.
Given piecewise function:
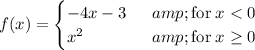
Therefore, the function has two definitions:
- f(x) = -4x - 3 when x is less than 0.
- f(x) = x² when x is greater than or equal to 0.
When graphing piecewise functions:
- Use an open circle where the value of x is not included in the interval.
- Use a closed circle where the value of x is included in the interval.
- Use an arrow to show that the function continues indefinitely in that direction.
First piece of the function
Substitute the endpoint x = 0 into the first piece of the function to find its y-coordinate:
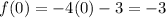
As the endpoint x = 0 is not included in the interval of this piece of the function, place an open circle at point (0, -3).
To help graph the line, find another point on the line by inputting another value of x that is less than 0 into the same function:
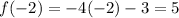
Draw a straight line from point (0, -3) through point (-2, 5) and add an arrow at the other endpoint to indicate the function continues indefinitely as x → -∞.
Second piece of the function
Substitute the endpoint x = 0 into the second piece of the function to find its y-coordinate:
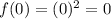
As the endpoint x = 0 is included in the interval of this piece of the function, place a closed circle at point (0, 0).
The graph of the function f(x) = x² is an upward-opening parabola with its vertex located at the origin (0, 0) and the y-axis serving as its axis of symmetry. As the interval for this piece of the function is x ≥ 0, the graph is the right side of the parabola.
To help graph the curve, find other points on the curve by inputting other values of x that are greater than 0 into the same function:
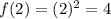
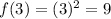
Draw a smooth curve from point (0, 0) through points (2, 4) and (3, 9) and add an arrow at the other endpoint to show that the function continues indefinitely as x → ∞.