Answer:
(a) Even
(b) Neither
Explanation:
Even and odd functions are special types of functions.
Even function
- f(-x) = f(x) for all values of x.
- Symmetric about the y-axis.
- Example even function: y = x²
Odd function
- f(-x) = -f(x) for any value of x.
- Symmetric about the origin.
- Example odd function: y = x³
To determine if a function is even, odd, or neither, we need to consider how the function behaves with respect to symmetry by replacing x with -x in the function and observing if the function remains unchanged (even function), becomes negative (odd function), or does something else (neither).
Part (a)
Given function:
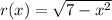
Replace the x with -x:
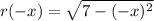
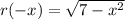
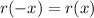
As (-x)² = x² for all values of x, then r(-x) = r(x) for all values of x.
Therefore, function r(x) is even.
Note: The graph of function r(x) is symmetric about the y-axis.
Part (b)
Given function:

Replace the x with -x:
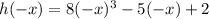
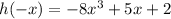
As h(-x) ≠ h(x) and h(-x) ≠ -h(x) for all values of x, function h(x) is neither an even function nor an odd function.
Note: The graph of function h(x) is not symmetric about origin.