Question

Precalculus Question

Answer 1

`\textsf{a)} \quad y = -(2)/(7)x - (11)/(7)`

`\textsf{b)} \quad y = 2x-1`

`\textsf{c)}\quad x = -(4)/(5)`

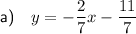
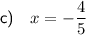
Explanation:

Part (a)

To find the equation of the line passing through the points (-2, -1) and (5, -3), first calculate its slope (m) using the slope formula:

`\boxed{\begin{array}{c}\underline{\sf Slope\; Formula}\\\\\textsf{Slope}\;(m)=(y_2-y_1)/(x_2-x_1)\\\\\textsf{where $(x_1,y_1)$ and $(x_2,y_2)$ are two points on the line.}\\\end{array}}`

Substitute the two points into the formula:

`m = (-3 - (-1))/(5 - (-2)) = (-3 + 1)/(5 + 2) = -(2)/(7)`

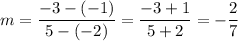
Now, substitute the slope (m) and one of the points (-2, -1) into the point-slope form of a linear equation, then rearrange the equation to isolate y to write the equation in slope-intercept form:

`\begin{aligned}y - y_1 &= m(x - x_1)\\\\y-(-1)&=-(2)/(7)(x-(-2))\\\\y+1&=-(2)/(7)(x+2)\\\\y+1&=-(2)/(7)x-(4)/(7)\\\\y&=-(2)/(7)x-(11)/(7)\end{aligned}`

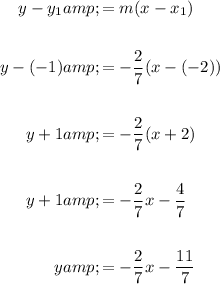
So, the equation of the line in slope-intercept form is:

`\large\boxed{\boxed{y = -(2)/(7)x - (11)/(7)}}`

`\hrulefill`

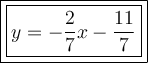
Part (b)

To find the equation of the line passing through (2, 3) and perpendicular to the line defined by 2x = -4y, we first need to find the slope of the given line.

Rearrange 2x = -4y to slope-intercept form:

`\begin{aligned}2x &= -4y\\\\4y&=-2x\\\\y&=(-2x)/(4)\\\\y&=-(1)/(2)x\end{aligned}`

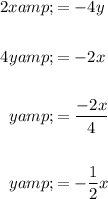
Therefore, the slope of the line is -1/2.

If two lines are perpendicular to each other, their slopes are negative reciprocals. Therefore, the slope (m) of the perpendicular line is:

`m = 2`

Now, substitute the found slope (m = 2) and the point the line passes through (2, 3) into the point-slope form of a linear equation, then rearrange the equation to isolate y to write the equation in slope-intercept form:

`\begin{aligned}y - y_1 &= m(x - x_1)\\\\y-3&=2(x-2)\\\\y-3&=2x-4\\\\y&=2x-1\end{aligned}`

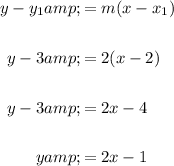
So, the equation of the line passing through (2, 3) and perpendicular to 2x = -4y is:

`\large\boxed{\boxed{y = 2x-1}}`

`\hrulefill`

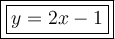
Part (c)

A line parallel to the y-axis is a vertical line.

Vertical lines have the equation of the form x = a, where a is a constant.

In this case, the line passes through the point (-4/5, 1/7), so the equation of the line is:

`\large\boxed{\boxed{x = -(4)/(5)}}`

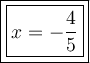
Note: There's no need to change this equation since it is already in a form that describes a vertical line parallel to the y-axis.