Question

100 POINTS! What are the coordinates of the point on the directed line segment from (−4−9) to (2,3) that partitions the segment into a ratio of 1 to 3?

Answer 1

`\left(-(5)/(2),-6\right)`

Explanation:

If we have two points, A(x₁, y₁) and B(x₂, y₂), and want to find a point C that partitions the line segment AB in the ratio m : n, where m and n are positive integers, we can use the following formula:

`C(x,y)=\left((mx_2+nx_1)/(m+n),(my_2+ny_1)/(m+n)\right)`

To find the coordinates of the point that partitions the directed line segment from (-4, -9) to (2, 3) into a ratio of 1 : 3, substitute the following values into the formula:

• (x₁, y₁) = (-4, -9)
• (x₂, y₂) = (2, 3)
• m = 1
• n = 3

Therefore:

`C(x,y)=\left((1(2)+3(-4))/(1+3),(1(3)+3(-9))/(1+3)\right)`

`C(x,y)=\left((2-12)/(4),(3-27)/(4)\right)`

`C(x,y)=\left((-10)/(4),(-24)/(4)\right)`

`C(x,y)=\left(-(5)/(2),-6\right)`

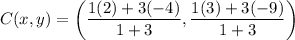
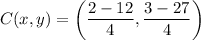
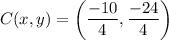
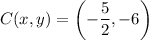
So, the coordinates of the point that partitions the segment into a 1 : 3 ratio are (-5/2, -6).