Question

what is the final angle θf that the ball's velocity vector makes with the negative y axis? express your answer in terms of some or all of the variables m , vi , θi , δt .

Answer 1

To find the final angle
`\( \theta_f \)` that the ball's velocity vector makes with the negative y-axis, we would typically follow these steps, assuming we are dealing with a projectile motion problem under the influence of gravity:

Step 1: Analyze the given variables and the motion.

-
`\( m \)` is the mass of the ball, but it does not affect the motion because, in projectile motion, all objects fall at the same rate regardless of their mass (ignoring air resistance).

-
`\( v_i \)` is the initial velocity of the ball.

-
`\( \theta_i \)`is the initial angle of the velocity vector with respect to the positive x-axis (assuming that's the standard interpretation).

-
`\( \delta t \)` is the time interval during which the motion takes place.

- Gravity acts downward, accelerating the ball with an acceleration of
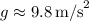`\( g \approx 9.8 \, \text{m/s}^2 \)` (if we're close to Earth's surface).

**Step 2: Break down the initial velocity into components.**

- The initial velocity in the x-direction is
`\( v_(ix) = v_i \cos(\theta_i) \).`

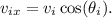
- The initial velocity in the y-direction is
`\( v_(iy) = v_i \sin(\theta_i) \).`

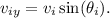
Step 3: Calculate the final velocity components.

- The final velocity in the x-direction,
`\( v_(fx) \)`, remains
`\( v_(ix) \)` since there is no horizontal acceleration in projectile motion.

- The final velocity in the y-direction,
`\( v_(fy) \)`, is affected by gravity and is calculated by
`\( v_(fy) = v_(iy) - g \cdot \delta t \)` (the negative sign indicates gravity is acting in the opposite direction to the initial y-component of velocity).

Step 4: Determine the final velocity vector.

- The final velocity vector
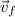`\( \vec{v}_f \)`has components
`\( v_(fx) \) and \( v_(fy) \).`

Step 5: Calculate the final angle
`\( \theta_f \)` with respect to the negative y-axis.

- The final angle
`\( \theta_f \)`can be found using the arctangent function:

`\[ \theta_f = \arctan\left((|v_(fx)|)/(|v_(fy)|)\right) \]`

- We take the absolute value of the velocity components because we are considering the angle with respect to the negative y-axis, and both velocity components could be positive or negative depending on the direction of motion.

Step 6: Adjust the angle if necessary.

- If the ball is still rising,
`\( v_(fy) \)` will be positive, and
`\( \theta_f \)` will be in the second quadrant.

- If the ball is falling,
`\( v_(fy) \)` will be negative, and
`\( \theta_f \)` will be in the fourth quadrant.