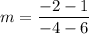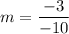Answer:
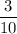
Explanation:
The slope of a line between two points
 and
and
 is defined as:
is defined as:

Note that the symbol
 just means "change in", so we are representing "rise" as
just means "change in", so we are representing "rise" as
 (change in y) and "run" as
(change in y) and "run" as
 (change in x).
(change in x).
From the given points
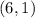 and
and
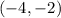 , we can identify the following variable values:
, we can identify the following variable values:
Now, we can plug these into the slope definition: