Question

Line DE bisects line AC at point B. AC = 5n - 5 and AB = 8n - 19. Find AC.

Answer 1

AC = 10

Explanation:

Given:

AC = 5n - 5

AB = 8n - 19

Since

DE bisects the line AC at point B.

Then AB is twice of AC.

So,

2AB = AC

Substitute the value

2(8n-19) = 5n - 5

Open bracket

16n - 38 = 5n - 5

Add 38 and subtract 5n on both sides

16n - 38+38-5n = 5n - 5 + 38-5n

Simplify:

11n = 33

`\sf n =(33)/(11)`

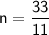
n = 3

Now

AC = 5n - 5

Substitute value of n.

AC= 5×3 - 5 = 15 -5 = 10

Therefore,

AC = 10