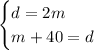Answer:
Explanation:
Let d be the amount of time Dan took to finish his homework (in minutes).
Let m be the amount of time Makiko took to finish her homework (in minutes).
We are told that it took Dan twice as long to finish his homework than Makiko did. This can be expressed as:
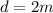
We are told that Dan took 40 minutes longer than Makiko did. This can be expressed as:
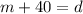
Therefore, the system of equations that could be used to determine the amount of time Dan took to finish his homework (d) and the amount of time it took Makiko to finish her homework (m) is: