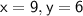Answer:
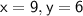
Explanation:
Before answering this question, we need to know about the co interior angle.
Co-interior angles are two interior angles of two parallel lines that lie on the same side of a transversal.
Properties of co-interior angles:
- Co-interior angles are supplementary, meaning that they add up to 180°.
- If two angles are supplementary, then the lines containing the angles must be parallel.
In this case:
We need to use it twice.
Since Co-interior angles are supplementary, meaning that they add up to 180°.
Using this:
For Upper Co-interior angle
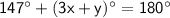
For lower co-interior angle

Now
Adding both equation, we get

Simplify like terms:
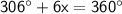
Subtract 306° on both side, we get
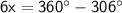
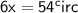
Divide both sides by 6.
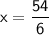

Substitute the value of x in any equation, we get
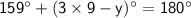

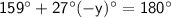
Simplify like terms:
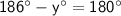
Add y and subtract 180° on both sides, we get
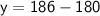

So,
answer is: