Question

Pls help this is really hard

Directions: Complete each trinomial so that it is a perfect square​

Answer 1

`\large\text{1.\quad$x^2+18x+\boxed{81}$}`

`\large\text{2.\quad$x^2+\boxed{4}\:x+4$}`

`\large\text{3.\quad$x^2-100x+\boxed{2500}$}`

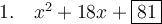
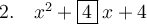
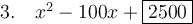
Explanation:

A perfect square trinomial is a type of quadratic trinomial (a polynomial with three terms) that can be factored into the square of a binomial expression in one of two forms: (ax + b)² or (ax - b)².

To complete each of the given trinomials so that they become perfect square trinomials, they should be in the form:

(ax + b)² = a²x² + 2abx + b²

(ax + b)² = a²x² - 2abx + b²

`\hrulefill`

Question 1

Given:

`x^2 + 18x + \boxed{\phantom{w}}`

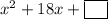
Since both operations are addition, we use the form (ax + b)².

Compare the coefficients of the given expression with a²x² + 2abx + b²:

`a^2 = 1 \implies a=1`

`2ab = 18`

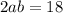
Substituting a = 1 into 2ab = 18 and solving for b:

`\begin{aligned}2 \cdot 1 \cdot b&=18\\2b&=18\\b&=9\end{aligned}`

As b = 9, then:

`b^2=9^2=81`

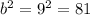
Therefore, the completed perfect square trinomial is:

`\large\text{$x^2 + 18x + \boxed{81}$}`

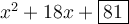
This trinomial can be factored as (x + 9)².

`\hrulefill`

Question 2

Given:

`x^2 + \boxed{\phantom{w}}\:x + 4`

Since both operations are addition, we use the form (ax + b)².

Compare the coefficients of the given expression with a²x² + 2abx + b²:

`a^2 = 1 \implies a=1`

`b^2=4\implies b=2`

Substituting a = 1 and b = 2 into 2ab:

`2ab=2(1)(2)=4`

Therefore, the completed perfect square trinomial is:

`\large\text{$x^2 + \boxed{4}\:x + 4$}`

This trinomial can be factored as (x + 2)².

`\hrulefill`

Question 3

Given:

`x^2 - 100x + \boxed{\phantom{w}}`

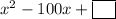
Since the first operation is subtraction and the second operation is addition, we use the form (ax - b)².

Compare the coefficients of the given expression with a²x² - 2abx + b²:

`a^2 = 1 \implies a=1`

`2ab = 100`

Substituting a = 1 into 2ab = 100 and solving for b:

`\begin{aligned}2 \cdot 1 \cdot b&=100\\2b&=100\\b&=50\end{aligned}`

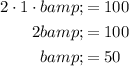
As b = 50, then:

`b^2=50^2=2500`

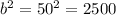
Therefore, the completed perfect square trinomial is:

`\large\text{$x^2 -100x + \boxed{2500}$}`

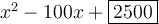
This trinomial can be factored as (x - 50)².