Question

How many solutions to 26

Answer 1

26. has one solution (i.e., x = -8)

Explanation:

We can begin solving using the following steps:

Step 1: Multiply both sides by the least common denominator (LCD):

Multiplying both sides by the LCD will allow us to clear the fractions.

We find the LCD by multiplying the denominators 2 and 3:

`LCD = 2*3\\LCD=6`

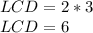
Since the LCD is 6, we multiply both sides by 6:

Multiplying the left-side by the LCD 6:

`6((4x+6)/(2))\\ \\(6(4x+6))/(2)\\ \\(24x+36)/(2)\\ \\12x+18`

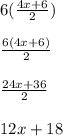
Multiplying the right-side by the LCD 6:

`6((3x-15)/(3))\\ \\(6(3x-15))/(3)\\ \\(18x-90)/(3)\\ \\6x-30`

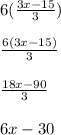
Thus, our equation without fractions is given by:

`12x+18=6x-30`

Step 2: Add 30 to both sides:

`(12x+18=6x-30)+30\\12x+48=6x`

Step 3: Subtract 12x from both sides:

`(12x+48=6x)-12x\\48=-6x`

Step 4: Divide both sides by -6 to solve for x:

`(48=-6x)/-6\\-8=x`

Thus, x = -8.

Optional Step 5: Check the validity of the answer:

We can check that our answer is correct by plugging in -8 for x in both sides of the equation and seeing if we get the same answer:

`(4(-8)+6)/(2)=(3(-8)-15)/(3)\\ \\ (-32+6)/(2)=(-24-15)/(3)\\ \\ (-26)/(2)=(-39)/(3)\\ \\ -13=-13`

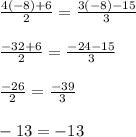
Thus, our answer for x is correct, so there's one solution to the equation in (26.)