Question

Use trigonometric identities to simplify
`sec^2(\pi /2-(x))[sin^2(x) -sin^4(x)]`

Answer 1

Explanation:

I am using trig identities and the formula for the difference of the cos of 2 angles to solve this. I'll do the steps one at a time. It's super tricky. First I'm just going to work on simplifying the sec² part and then I'll introduce the sin²(x) - sin⁴(x) when I need it. Beginning with the identity for the difference of the cos of 2 angles, knowing that sec²(x) =
`(1)/(cos^2(x))`:

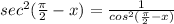`sec^2((\pi)/(2)-x)=(1)/(cos^2((\pi)/(2)-x ))` and expand that using the formula for the difference:

`(1)/(cos((\pi)/(2)-x)cos((\pi)/(2)-x) )=`
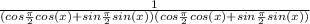`(1)/((cos(\pi)/(2)cos(x)+sin(\pi)/(2)sin(x))(cos(\pi)/(2)cos(x)+sin(\pi)/(2)sin(x)) )` and all of that simplifies down to

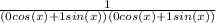`(1)/((0cos(x)+1sin(x))(0cos(x)+1sin(x)))` which simplifies further to

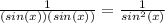`(1)/((sin(x))(sin(x)))=(1)/(sin^2(x))` Now we'll bring in the other term. This is what we have now:

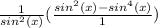`(1)/(sin^2(x))((sin^2(x)-sin^4(x))/(1))` and distribute in to get:

`(sin^2(x))/(sin^2(x))-(sin^4(x))/(sin^2(x))` which simplifies to

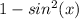`1-sin^2(x)` and that, finally, simplifies down to a simple

`cos^2(x)`