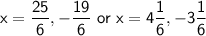Answer:
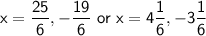
Explanation:
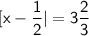
In order to solve the equation, we can follow these steps:
Convert an improper fraction to proper fraction:

Now, rewrite the equation with the proper fraction on the right-hand side:

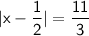
We'll have two cases to consider, one for when the expression inside the absolute value is positive and one for when it's negative.
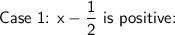
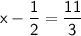
Now, solve for x.
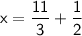
To add these fractions, find a common denominator, which is 6:
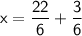
Combine t
ki. he fractions:
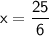
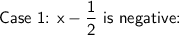
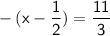
First, distribute the negative sign on the left side:
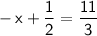
Now, isolate x:
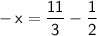
To subtract these fractions, find a common denominator, which is 6:
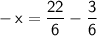
Combine the fractions:
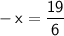
Now, multiply both sides by -1 to solve for x:
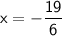
So, the solutions to the equation are: