Answer:
Yes, I agree
Explanation:
For the cubic function
A cubic function is represented as:
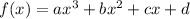
A cubic function may have 1, 2 or 3 x intercepts. This is shown below
For 3 x intercepts
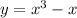
Equate y to 0
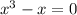
Expand
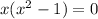
Express
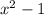 as difference of two squares
as difference of two squares

x = 0 or 1 or -1
For 2 x intercepts
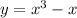

Equate y to 0
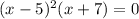
Expand
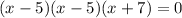
x= 5 or x = -7
For 1 x intercept
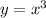
Equate y to 0

Take cube roots of both sides
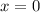
It has been shown above that a cubic function may have 1, 2 or 3.
So, I agree to the statement
For the quadratic function
A quadratic function will not have any x intercept when the function can not be factorized;
E.g.

The above function has no x intercept.
A quadratic function will have at least 1 x intercept when the function can be factorized;
E.g.
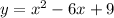
Equate y to 0
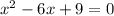
Expand
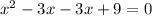

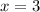
We've shown that a quadratic may have no x intercept, and it may also have x intercept(s)
Hence, I agree to both statement